From classroom blackboards to fieldwork notebooks, many problems turn on knowing not just how large a measurement is but which way it points. Directional quantities appear throughout mechanics, electromagnetism and navigation, so a compact list is handy when you need a quick reminder during study or calculation.
There are exactly 31 Vector Quantities, ranging from Acceleration to Weight. For each entry the data are organized with Symbol,SI unit,Typical contexts; you’ll find them below.
How can I tell if a quantity is a vector or a scalar?
A vector has both magnitude and direction, while a scalar has only magnitude; look for descriptions that specify direction (e.g., “to the east” or “upward”) or use arrows/bold notation in formulas. Examples like Acceleration and Weight are vectors, and checking whether quantities combine by direction-sensitive rules (vector addition, components) is a quick practical test.
What’s the best way to use the Symbol, SI unit, and Typical contexts columns when studying?
Use the Symbol column to recognize variable names, the SI unit to check dimensional consistency in equations, and Typical contexts to see how a quantity is applied; practice by picking a few entries (for example Acceleration and Weight), writing their symbols and units, and solving simple problems that require resolving components or applying vector addition.
Vector Quantities
| Name | Symbol | SI unit | Typical contexts |
|---|---|---|---|
| Displacement | Δr or r | m | Kinematics, navigation, path planning |
| Position | r | m | Coordinate systems, mechanics, fields |
| Velocity | v | m/s | Motion analysis, traffic, fluids |
| Acceleration | a | m/s^2 | Dynamics, free-fall, vehicle design |
| Jerk | j | m/s^3 | Ride comfort, control systems, robotics |
| Linear momentum | p | kg·m/s | Collisions, mechanics, conservation laws |
| Impulse | J | N·s | Collisions, impact analysis, sports |
| Force | F | N | Statics, dynamics, engineering |
| Weight | W or mg | N | Gravity problems, load calculations |
| Torque (Moment) | τ | N·m | Rotational mechanics, engines, wrenches |
| Angular momentum | L | kg·m^2/s | Rotational dynamics, orbital motion |
| Angular velocity | ω | rad/s | Rotations, rigid body motion, robotics |
| Angular acceleration | α | rad/s^2 | Rotational dynamics, motors |
| Electric field | E | V/m (or N/C) | Electrostatics, circuits, particle accelerators |
| Magnetic flux density (magnetic field) | B | T | Electromagnetism, motors, MRI |
| Magnetic field strength | H | A/m | Magnetics, material magnetization |
| Electric displacement field | D | C/m^2 | Dielectrics, capacitor design, electrodynamics |
| Electric dipole moment | p | C·m | Molecules, dielectrics, spectroscopy |
| Magnetic dipole moment | μ | A·m^2 | Magnets, loops, atomic spins |
| Current density | J | A/m^2 | Conductors, plasmas, electromagnetics |
| Poynting vector | S | W/m^2 | Electromagnetic waves, radiation power flow |
| Vector potential | A | V·s/m (or T·m) | Electrodynamics, quantum mechanics |
| Polarization (electric) | P | C/m^2 | Dielectrics, optics, materials |
| Magnetization | M | A/m | Magnetic materials, ferromagnets |
| Gravitational field | g | m/s^2 | Astrophysics, geophysics, engineering |
| Vorticity | ω (or ∇×v) | s^-1 | Fluid dynamics, turbulence, aerodynamics |
| Wave vector | k | rad/m | Waves, optics, quantum mechanics |
| Heat flux | q | W/m^2 | Thermal conduction, heat exchangers |
| Surface traction (stress vector) | t | N/m^2 | Continuum mechanics, contact forces |
| Mass flux (mass current density) | j_m | kg/(m^2·s) | Fluid transport, convection, porous media |
| Momentum density | p_density | kg/(m^2·s) | Fluid dynamics, field theories |
Images and Descriptions

Displacement
Vector from an object’s initial to final position indicating net motion with magnitude and direction. Useful in kinematics and navigation; unlike distance, displacement records direction. Example: 100 m east from start denotes displacement, not total path length.

Position
Vector locating a point relative to an origin. It gives both distance and direction from a chosen origin, used to describe particle locations, field points, and to compute displacement or potential at that point.

Velocity
Rate of change of position: a vector describing how fast and in which direction an object moves. Average and instantaneous velocities indicate directionality of motion. Example: 20 m/s north is a velocity.

Acceleration
Rate of change of velocity with respect to time, showing how speed or direction change. Acceleration explains forces via Newton’s laws; example: 9.81 m/s^2 downward for near-Earth free fall.

Jerk
Third time derivative of position; rate of change of acceleration. Jerk matters for smooth motion control, passenger comfort, and mechanical stress when acceleration changes abruptly.
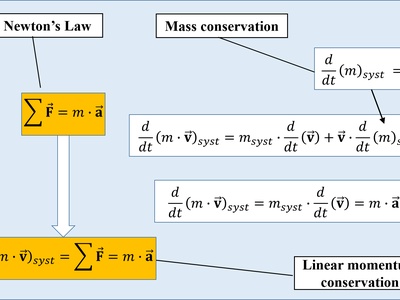
Linear momentum
Product of mass and velocity; a conserved vector in closed systems. Momentum indicates motion quantity and direction; used in collision analysis and impulse-momentum calculations.

Impulse
Integral of force over time; gives change in momentum. Impulse describes how a force applied briefly alters an object’s motion, like a bat striking a ball.

Force
Push or pull causing acceleration; a fundamental vector in Newtonian mechanics. Forces determine motion, equilibrium, and deformation. Example: 10 N upward applied to lift an object.

Weight
Force due to gravity on a mass; vector pointing toward the local gravitational center. Weight determines apparent heaviness and supports needed for structures and vehicles.

Torque (Moment)
Measure of a force’s ability to produce rotation about a point or axis. Torque vector direction follows right-hand rule; used for turning bolts, engine output, and stability.

Angular momentum
Rotational analogue of linear momentum; product of moment of inertia and angular velocity or r×p. Conserved in isolated systems; explains gyroscope behavior and planetary orbits.

Angular velocity
Rate and axis of rotation; a vector whose magnitude is rotation speed and direction is along the rotation axis (right-hand rule). Used in kinematics of spinning objects and control systems.

Angular acceleration
Rate of change of angular velocity; indicates how rotational speed and axis orientation change over time. Drives torque requirements for accelerating wheels and rotors.
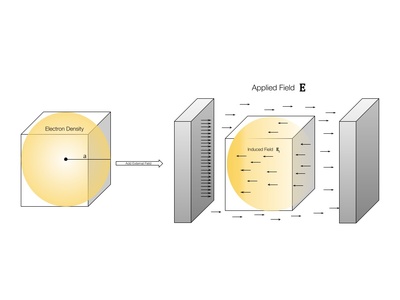
Electric field
Vector field describing force per unit charge on a test charge. Electric fields determine charge motion and interactions; example: field between capacitor plates directs charges.
Magnetic flux density (magnetic field)
Vector describing magnetic influence on moving charges and magnetic materials. B determines Lorentz forces on charges and torque on magnets; measured in tesla.

Magnetic field strength
Field related to sources (currents, magnets) in materials; H links externally applied magnetizing forces to material response, often used in magnetic circuit calculations.

Electric displacement field
Vector field accounting for free charge and polarization in materials. D simplifies boundary-value problems in media; in vacuum it equals ε0E.
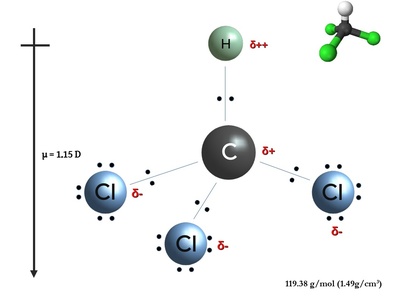
Electric dipole moment
Vector from negative to positive charge separation; measures strength and orientation of a dipole. Determines torque in electric fields and interaction energies in chemistry and materials.

Magnetic dipole moment
Vector quantifying strength and orientation of a magnetic source like a current loop or atom. Determines torque in external magnetic fields and interaction energies between magnets.
Current density
Vector field giving electric current per unit area at a point; direction follows charge flow. J enters Maxwell’s equations and Ohm’s law for spatially varying currents.

Poynting vector
Vector representing power flow density carried by electromagnetic fields; points in direction of energy transport. Useful for antenna radiation, waveguides, and energy transfer analysis.

Vector potential
Mathematical vector whose curl gives magnetic flux density B. A is central in gauge theories and quantum effects like the Aharonov–Bohm effect despite not always being directly measurable.
Polarization (electric)
Vector field describing dipole moment per unit volume in a material. Polarization measures how a material responds to an electric field and affects capacitance and wave propagation.

Magnetization
Vector field giving magnetic dipole moment per unit volume in a material. Magnetization describes intrinsic magnetic ordering and influences internal magnetic fields and hysteresis.

Gravitational field
Vector field giving gravitational acceleration at each point; tells how masses accelerate under gravity. Near Earth g≈9.81 m/s^2 downward; used in orbits and weight calculations.

Vorticity
Local rotation of a fluid parcel defined as the curl of velocity. Vorticity indicates swirling strength and direction; used to analyze eddies, vortices, and aerodynamic lift mechanisms.

Wave vector
Vector indicating direction of wave propagation and spatial frequency; magnitude equals 2π/λ. Wave vector appears in dispersion relations and interference analysis.

Heat flux
Vector describing heat energy transfer per unit area per time; direction is from hot to cold. Used in Fourier’s law to model temperature distributions and cooling design.

Surface traction (stress vector)
Vector giving force per unit area acting on a surface element inside a material, combining normal and shear stress components. Essential for boundary conditions and failure analysis.

Mass flux (mass current density)
Vector quantifying mass flow per unit area per time, equal to density times velocity. Used in continuity equations and transport problems in fluids and mixtures.
Momentum density
Vector field giving linear momentum per unit volume in a medium (density×velocity). Helps express conservation laws and relate stresses to momentum transport.






