From logic seminars to software design reviews, the formal sciences supply the language and methods we use to model, prove, and reason about abstract systems. They show up in classrooms, research labs, and engineering teams whenever structure and rigorous argument matter.
There are 38 Branches of Formal Science, ranging from Abstract Algebra to Type Theory; for each, entries are organized by Core focus, Main methods, Common applications — you’ll find below.
How do branches of the formal sciences differ from natural or social sciences?
Formal sciences focus on abstract systems, definitions, and proofs rather than empirical observation. Their methods are axiomatic reasoning, formal modeling, and computation; applications appear in designing algorithms, verifying software, and shaping theoretical foundations used across natural and social sciences.
Which branch is best if I want to work on computing and formal proofs?
Look to logic, discrete mathematics, type theory, and formal methods—each combines theory with practical tools for specifying and verifying systems. Start with an introductory course (proofs, discrete math, or logic), follow with programming and proof assistants (Coq, Lean), and build small verification projects.
Branches of Formal Science
| Name | Core focus | Main methods | Common applications |
|---|---|---|---|
| Logic | Valid reasoning and formal inference | Axiomatic systems, formal languages, semantic and syntactic proofs, truth tables. | Philosophy, mathematics, computer science, linguistics, artificial intelligence foundations. |
| Mathematical Logic | Formalizing logical reasoning within mathematics | Set theory, model theory, proof theory, and computability theory methods. | Foundations of mathematics, theoretical computer science, automated theorem proving. |
| Set Theory | Study of collections of objects (sets) | Axiomatic systems (ZFC), logical deduction, transfinite induction, formal proofs. | Foundation of all mathematics, database theory, theoretical computer science, linguistics. |
| Proof Theory | Formal proofs as mathematical objects | Structural proof theory, ordinal analysis, reverse mathematics, proof complexity analysis. | Automated theorem proving, software verification, mathematical foundations, logic programming. |
| Model Theory | Study of mathematical structures and logic | First-order logic, elementary equivalence, type spaces, quantifier elimination. | Algebraic geometry, number theory, database theory, proving mathematical consistency. |
| Computability Theory | What problems can be solved by algorithms | Turing machines, recursive functions, lambda calculus, formal undecidability proofs. | Understanding computation limits, proving problem unsolvability, computer science theory. |
| Modal Logic | Reasoning about necessity and possibility | Kripke semantics (possible worlds), axiomatic systems, tableau methods. | Philosophy, artificial intelligence, game theory, computer science (verification), linguistics. |
| Mathematics | Quantity, structure, space, and change | Logical deduction from axioms, proof, abstraction, modeling, and computation. | Science, engineering, finance, computer science, medicine, social sciences. |
| Algebra | Mathematical symbols and their manipulation rules | Axiomatic method, group theory, ring theory, field theory, linear transformations. | Cryptography, physics, computer graphics, coding theory, engineering, chemistry. |
| Linear Algebra | Vectors, vector spaces, and linear mappings | Matrix operations, vector space axioms, determinants, eigenvalues, Gaussian elimination. | Computer graphics, machine learning, physics, engineering, data analysis. |
| Abstract Algebra | Algebraic structures like groups, rings, fields | Axiomatic deduction, Galois theory, representation theory, homological algebra. | Cryptography, particle physics, number theory, coding theory, computer science. |
| Number Theory | Properties and relationships of integers | Modular arithmetic, prime factorization, Diophantine equations, analytic methods. | Cryptography (e.g., RSA), computer security, coding theory, pure mathematics. |
| Geometry | Properties of space, shape, size, figures | Axiomatic systems (Euclidean and non-Euclidean), coordinate systems, transformations. | Physics (relativity), computer-aided design (CAD), art, architecture, robotics. |
| Topology | Properties of space preserved under deformation | Set theory, point-set methods, algebraic invariants, knot theory. | Data analysis, string theory, robotics, molecular biology, network analysis. |
| Combinatorics | Counting, arrangement, and combination of objects | Enumeration, graph theory, combinatorial design, optimization, probabilistic methods. | Computer science (algorithms), statistics, logistics, network design, bioinformatics. |
| Graph Theory | Study of graphs as mathematical structures | Vertex and edge analysis, algorithms (e.g., Dijkstra’s), matrix representations. | Social networks, logistics, computer networks, bioinformatics, circuit design. |
| Game Theory | Mathematical models of strategic interaction | Equilibrium analysis (Nash), optimization, probability, axiomatic set theory. | Economics, political science, biology (evolution), computer science (AI), business strategy. |
| Analysis | Continuous change, limits, and related theories | Limits, derivatives, integrals (calculus), series, measure theory, metric spaces. | Physics, engineering, finance, signal processing, differential equations. |
| Differential Equations | Equations involving functions and their derivatives | Integration, numerical methods, transform methods (Laplace, Fourier), qualitative analysis. | Physics, engineering, biology, economics, chemistry, population modeling. |
| Numerical Analysis | Algorithms for numerical approximation | Iteration methods, interpolation, discretization, finite element analysis, optimization. | Scientific computing, engineering simulation, financial modeling, weather forecasting. |
| Probability Theory | Mathematical study of random phenomena | Measure theory, stochastic processes, combinatorial analysis, limit theorems. | Statistics, finance, machine learning, physics, insurance (actuarial science). |
| Statistics | Collection, analysis, and interpretation of data | Estimation, hypothesis testing, regression, Bayesian inference, probability theory. | Scientific research, business analytics, medicine, public policy, machine learning. |
| Mathematical Statistics | The mathematical foundations of statistics | Probability theory, decision theory, measure theory, asymptotic theory. | Development of new statistical methods, machine learning theory, econometrics. |
| Stochastic Processes | Models for systems evolving randomly over time | Markov chains, Brownian motion, martingale theory, queuing theory, random walks. | Finance (stock prices), physics, biology, telecommunications, operations research. |
| Information Theory | Quantification, storage, and communication of information | Probability theory, entropy, channel coding theorem, source coding, statistics. | Telecommunications, data compression, computer science, machine learning, neuroscience. |
| Theoretical Computer Science | Mathematical foundations of computation and information | Formal proofs, automata theory, complexity theory, algorithms, logic. | Algorithm design, programming languages, cryptography, artificial intelligence. |
| Algorithms and Data Structures | The study of computational methods | Asymptotic analysis, design patterns (e.g., divide and conquer), complexity theory. | Software development, bioinformatics, logistics, search engines, scientific computing. |
| Automata Theory | Abstract machines and computational problems | Finite automata, pushdown automata, Turing machines, formal grammars. | Compiler design, natural language processing, software verification, text parsing. |
| Formal Languages | Languages with precise description rules | Formal grammars (Chomsky hierarchy), regular expressions, automata theory. | Compiler construction, programming language design, linguistics, text processing. |
| Computational Complexity Theory | Classifying computational problems by resource usage | Asymptotic notation (Big O), reduction, complexity classes (P, NP), proofs. | Algorithm design, cryptography, optimization, understanding problem difficulty. |
| Cryptography (Theoretical) | Formal study of secure communication techniques | Number theory, complexity theory, probability, information theory, formal proofs. | Data security, digital signatures, cryptocurrency, secure communications. |
| Programming Language Theory | Design, analysis, and classification of programming languages | Type theory, operational semantics, denotational semantics, lambda calculus. | Compiler design, new language development, software verification, static analysis. |
| Formal Methods | Mathematically-based techniques for software/hardware specification | Model checking, theorem proving, abstract interpretation, formal specification. | Safety-critical systems (aerospace, medical), hardware verification, software security. |
| Type Theory | Formal systems where every term has a “type” | Lambda calculus, dependent types, logical frameworks, constructive mathematics. | Programming language design, proof assistants (Coq, Agda), foundations of mathematics. |
| Lambda Calculus | A formal system for expressing computation | Variable binding, substitution, reduction rules (alpha, beta, eta). | Programming language theory (functional programming), proof theory, computability. |
| Category Theory | Abstract study of mathematical structures and relationships | Functors, natural transformations, limits and colimits, adjoints, diagrams. | Functional programming, algebraic topology, logic, theoretical computer science. |
| Systems Theory | Interdisciplinary study of complex systems | Mathematical modeling, feedback loops, emergent behavior analysis, network theory. | Engineering, biology, sociology, management, ecology, computer science. |
| Control Theory (Mathematical) | Mathematical analysis and design of dynamical systems | Differential equations, state-space representation, stability analysis, optimization. | Robotics, aerospace engineering, process control, economics, autonomous vehicles. |
Images and Descriptions

Logic
Logic provides the foundational rules for reasoning and argument. It uses formal languages to construct valid proofs, determining what conclusions logically follow from a set of premises. It’s the bedrock of mathematics, computer programming, and rational thought, ensuring consistency and correctness.
Mathematical Logic
This field applies the rigorous methods of mathematics to the study of logic itself. It formalizes concepts of proof, truth, and computability, exploring the deep connections between mathematical structures and the logical languages used to describe them, forming the foundation of modern math.
Set Theory
Set theory is the mathematical language used to define and construct almost all other mathematical objects. It deals with the nature of collections, both finite and infinite, providing the fundamental axioms upon which concepts like numbers, functions, and geometric spaces are built.
Proof Theory
Proof theory analyzes the structure and properties of mathematical proofs themselves. Instead of just using proofs to establish truth, it treats them as formal objects to study, leading to insights about consistency, complexity, and what can be proven within a given logical system.

Model Theory
Model theory is the bridge between formal languages and mathematical structures (or “models”). It investigates how logical sentences are interpreted in different mathematical contexts, allowing mathematicians to transfer results between different areas and understand the expressive power of logical systems.

Computability Theory
Also known as recursion theory, this branch explores the absolute limits of what can be computed. Using abstract models like the Turing machine, it formally proves that certain problems are impossible to solve with any computer, no matter how powerful, defining the boundary of algorithmic solvability.
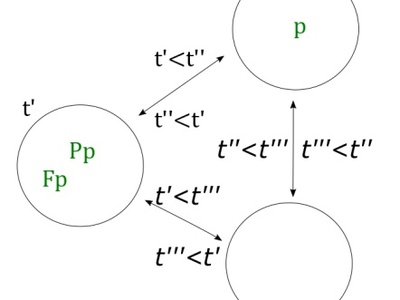
Modal Logic
Modal logic extends classical logic to handle concepts like possibility, necessity, belief, and time. By introducing “modal operators,” it provides a powerful formal framework for analyzing statements that go beyond simple true or false, such as what could be or must be true.

Mathematics
Mathematics is the abstract study of topics encompassing numbers, structure, space, and change. It uses rigorous logic to develop and prove theorems from a set of axioms, creating a universal language to describe and solve problems across countless other disciplines.

Algebra
Algebra is the study of mathematical symbols and the rules for manipulating them. It generalizes arithmetic by using variables to represent unknown quantities, allowing for the systematic solution of equations and the study of abstract structures like groups, rings, and fields.

Linear Algebra
Linear algebra is the study of linear equations and their representations in vector spaces and matrices. It is a cornerstone of modern mathematics, essential for modeling and solving systems of equations that appear in fields from 3D graphics to quantum mechanics and data science.

Abstract Algebra
Abstract algebra studies algebraic structures in their own right, independent of specific numbers. By defining objects like groups and rings through a set of axioms, it uncovers deep structural properties that are fundamental to cryptography, physics, and advanced mathematics.
Number Theory
Often called “the queen of mathematics,” number theory is the study of the integers. It explores the fascinating properties of prime numbers, rational numbers, and integer equations, leading to elegant and profound results that are surprisingly critical for modern digital security and cryptography.

Geometry
Geometry is the branch of mathematics concerned with questions of shape, size, the relative position of figures, and the properties of space. From ancient Euclidean geometry to modern non-Euclidean spaces used in relativity, it provides the framework for understanding our physical world.

Topology
Topology studies properties of geometric objects that are unchanged by continuous deformations like stretching or bending, but not tearing. Often called “rubber-sheet geometry,” it classifies shapes based on fundamental characteristics like connectivity, providing powerful tools for abstract analysis and data science.

Combinatorics
Combinatorics is the art and science of counting and arranging. It addresses problems about how many ways there are to form a particular structure or whether a certain arrangement is possible, making it fundamental to algorithm analysis, network optimization, and probability.
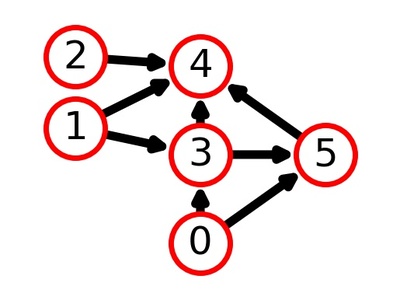
Graph Theory
Graph theory models relationships between objects. It represents entities as “nodes” and their connections as “edges,” allowing for the formal analysis of networks. This makes it indispensable for optimizing routes, understanding social networks, and designing efficient computer and communication systems.

Game Theory
Game theory is the formal study of decision-making where multiple players must make choices that influence one another’s outcomes. It analyzes strategies, conflict, and cooperation, providing a mathematical framework for understanding situations from market competition to international relations.

Analysis
Mathematical analysis grew from the rigorous formulation of calculus and deals with concepts of limits, continuity, and infinite processes. It provides the theoretical foundation for modeling continuous change, making it essential for virtually all of modern science and engineering.

Differential Equations
Differential equations describe how quantities change over time or space. They are the mathematical language of the natural sciences, used to model everything from planetary motion and fluid dynamics to population growth and the spread of disease, allowing us to predict system behavior.

Numerical Analysis
Numerical analysis develops and studies algorithms for solving mathematical problems that cannot be solved exactly. It provides methods for approximating solutions with high accuracy, forming the backbone of all computer-based simulations in science, engineering, and finance.

Probability Theory
Probability theory provides the mathematical framework for quantifying uncertainty and randomness. It uses axioms to define and calculate the likelihood of events, forming the theoretical basis for statistics, risk analysis, and any field that deals with unpredictable outcomes.

Statistics
Statistics is the science of learning from data. It involves the entire process of designing studies, collecting and analyzing data, and interpreting the results to make inferences about the world. It provides the essential tools for making decisions in the face of uncertainty.

Mathematical Statistics
This branch applies rigorous mathematical theory to the practice of statistics. It is concerned with the theoretical properties of statistical methods, using probability and analysis to prove why certain estimators or tests work, which is crucial for developing new, more powerful techniques.
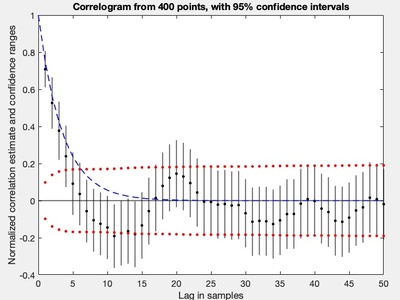
Stochastic Processes
A stochastic process is a model for a sequence of random events. This field studies the dynamics of systems that evolve over time in a probabilistic manner, providing powerful tools for modeling financial markets, particle movement, and customer arrival queues.
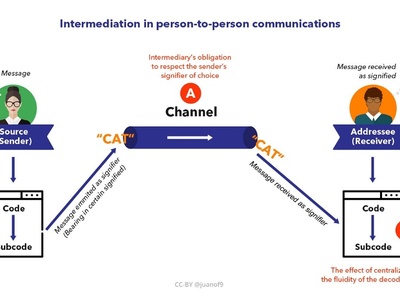
Information Theory
Developed by Claude Shannon, information theory provides a mathematical basis for communication. It defines and quantifies “information” using concepts like entropy, establishing the fundamental limits on how much data can be reliably compressed and transmitted over a noisy channel.
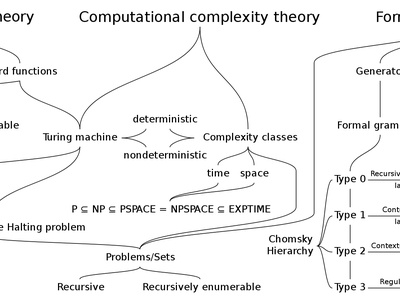
Theoretical Computer Science
This field provides the mathematical backbone for computer science. It explores the fundamental capabilities and limitations of computation, covering everything from what defines an algorithm to how efficiently a problem can be solved and how programming languages should be designed.
Algorithms and Data Structures
This core area of computer science is the formal study of how to efficiently organize data and devise step-by-step procedures (algorithms) to solve computational problems. Its principles are universal, underlying virtually every piece of software ever written, from operating systems to web applications.
Automata Theory
Automata theory is the study of abstract computing devices, or “automata.” By defining simple machines with strict rules, it helps classify which problems can be solved within certain computational limits, forming the theoretical basis for compilers and text-processing software.

Formal Languages
In this context, a “language” is a set of strings defined by strict mathematical rules. This field classifies different types of formal languages and the abstract machines that can recognize them, providing the theoretical underpinnings for programming languages and compilers.
Computational Complexity Theory
This branch classifies computational problems according to their inherent difficulty. By analyzing the time and memory resources required to solve them, it distinguishes between “easy” (P) and “hard” (NP) problems, a distinction that is fundamental to cryptography and algorithm design.

Cryptography (Theoretical)
Theoretical cryptography applies mathematical principles to design and analyze protocols that prevent third parties from reading private messages. It uses concepts from number theory and complexity theory to build provably secure systems for encryption, authentication, and other information security tasks.

Programming Language Theory
Often called PLT, this field uses formal mathematics to study the design, implementation, and analysis of programming languages. It provides a rigorous framework for defining language features and proving properties about programs, such as type safety, which helps create more reliable software.

Formal Methods
Formal methods apply mathematical logic and other formalisms to the design and verification of software and hardware systems. By creating a precise mathematical model of a system, it’s possible to rigorously prove its correctness, which is crucial for high-stakes applications like flight control systems.

Type Theory
Type theory is the study of systems that classify values and expressions into “types.” Originally a tool to avoid paradoxes in logic, it is now a central part of modern programming language design, where it’s used to prevent bugs by ensuring code is logically consistent.
Lambda Calculus
Lambda calculus is a minimalist but universal model of computation based on function abstraction and application. Developed by Alonzo Church, it provides a foundational language for expressing any computable function and is the theoretical basis for functional programming languages like Lisp and Haskell.
Category Theory
Category theory is a high-level abstraction that formalizes mathematical structures and the relationships between them. By focusing on “objects” and “morphisms” (arrows), it unifies concepts from different areas of mathematics and computer science, revealing deep and often surprising connections.
Systems Theory
Systems theory investigates the abstract principles that govern how systems of interconnected parts behave. Rather than focusing on the parts themselves, it studies their organization, interactions, and emergent properties, providing a holistic framework applicable to nearly any complex entity.

Control Theory (Mathematical)
Mathematical control theory provides the formal foundation for designing systems that behave in a desired manner. It uses differential equations and optimization to create controllers that manage and stabilize dynamic systems, from cruise control in a car to the flight path of a spacecraft.