From gemstone veins to cutting-edge labs, the way atoms stack in a solid controls color, strength and electrical behavior. Spotting those patterns helps scientists and engineers predict how a material will perform in real conditions.
There are 32 Types of Crystal Structures, ranging from Antifluorite to Zincblende (ZnS). For each, you’ll find below Crystal system (Bravais lattice),Coordination number,Typical materials.
How can I identify a material’s crystal structure quickly?
The fastest practical method is X-ray diffraction (XRD) — it gives a fingerprint of lattice spacing and symmetry; electron diffraction and high-resolution TEM are alternatives for tiny samples, while simple density measurements and known composition can narrow possibilities before running instrumental analysis.
Do crystal structures change with temperature or composition?
Yes — many materials undergo phase transitions (polymorphism) when heated, cooled or alloyed, so the same substance can adopt different structures (and properties) under different conditions; monitoring temperature, pressure and stoichiometry is key when predicting which structure you’ll find below.
Types of Crystal Structures
| Name | Crystal system (Bravais lattice) | Coordination number | Typical materials |
|---|---|---|---|
| Cubic | Three equal axes at 90° angles. | Varies | Iron, Copper, Salt (NaCl), Diamond |
| Tetragonal | Three axes at 90°, two are equal. | Varies | Rutile (TiO2), Zircon, Wulfenite |
| Orthorhombic | Three unequal axes at 90° angles. | Varies | Topaz, Sulfur, Aragonite (CaCO3) |
| Hexagonal | Three equal axes at 120°, one axis at 90°. | Varies | Graphite, Zinc, Beryl, Quartz |
| Trigonal | Three equal axes, equal non-90° angles. | Varies | Calcite, Corundum (Ruby, Sapphire), Tourmaline |
| Monoclinic | Three unequal axes, two at 90°. | Varies | Gypsum, Talc, Feldspar, Sugar |
| Triclinic | Three unequal axes, all non-90° angles. | Varies | Turquoise, Kaolinite, Plagioclase feldspars |
| Simple Cubic (P) | Cubic (Primitive) | 6 | Polonium (Po) |
| Body-Centered Cubic (BCC) | Cubic (Body-Centered) | 8 | Iron (α-Fe), Chromium, Tungsten |
| Face-Centered Cubic (FCC) | Cubic (Face-Centered) | 12 | Copper, Gold, Aluminum, Silver |
| Simple Tetragonal | Tetragonal (Primitive) | 6 | Not applicable |
| Body-Centered Tetragonal | Tetragonal (Body-Centered) | 8 | Indium, metastable Iron |
| Simple Orthorhombic | Orthorhombic (Primitive) | 6 | Sulfur (α-form), Gallium (metastable) |
| Base-Centered Orthorhombic | Orthorhombic (Base-Centered) | 4 | Not applicable |
| Body-Centered Orthorhombic | Orthorhombic (Body-Centered) | 8 | Uranium (α-form), Iodine |
| Face-Centered Orthorhombic | Orthorhombic (Face-Centered) | 12 | Neptunium (α-form), some alloys |
| Hexagonal | Hexagonal (Primitive) | 12 | Graphite, Magnesium, Zinc |
| Rhombohedral | Trigonal (Primitive) | Varies | Arsenic, Bismuth, Antimony |
| Simple Monoclinic | Monoclinic (Primitive) | 6 | Not applicable |
| Base-Centered Monoclinic | Monoclinic (Base-Centered) | 4 | Clinohedrite |
| Triclinic | Triclinic (Primitive) | Varies | Not applicable |
| Hexagonal Close-Packed (HCP) | Hexagonal (Primitive) | 12 | Magnesium, Titanium, Zinc, Cobalt |
| Diamond Cubic | Cubic (FCC) | 4 | Diamond (C), Silicon (Si), Germanium (Ge) |
| Rocksalt (NaCl) | Cubic (FCC) | 6 | NaCl, MgO, LiF, PbS |
| Cesium Chloride (CsCl) | Cubic (Simple) | 8 | CsCl, CsBr, TlCl |
| Zincblende (ZnS) | Cubic (FCC) | 4 | ZnS, GaAs, SiC, InP |
| Wurtzite (ZnS) | Hexagonal (Primitive) | 4 | ZnS, GaN, ZnO, CdS |
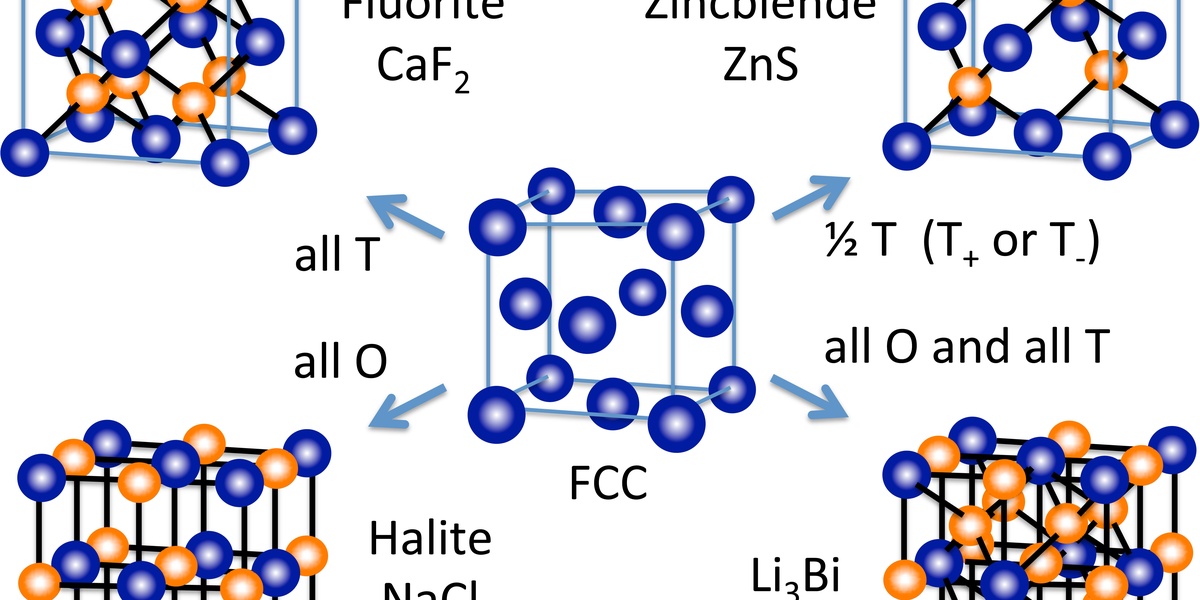
| Fluorite (CaF2) | Cubic (FCC) | 8 | CaF2, UO2, ZrO2, BaCl2 |
| Antifluorite | Cubic (FCC) | 4 | K2O, Li2S, Na2Se, K2S |
| Perovskite (ABX3) | Cubic (Simple) | 12 | CaTiO3, BaTiO3, many functional ceramics |
| Spinel (AB2O4) | Cubic (FCC) | Varies | MgAl2O4, Fe3O4 (Magnetite) |
| Rutile (TiO2) | Tetragonal (Primitive) | 6 | TiO2, SnO2, MnF2, MgF2 |
Images and Descriptions

Cubic
The most symmetric crystal system, where all sides of the unit cell are equal length and all angles are 90°. It resembles a perfect cube and is found in many common metals and minerals.

Tetragonal
Imagine stretching or compressing a cube along one axis; that’s a tetragonal system. It has one unique axis length, while the other two are equal, with all angles remaining 90°.

Orthorhombic
This system is like a rectangular box or a brick, where all three axes are of different lengths but all angles are 90°. It is a very common crystal geometry in minerals.

Hexagonal
Defined by its six-fold rotational symmetry around one axis. The unit cell is a prism with a hexagonal base, leading to the characteristic hexagonal shapes of its crystals.

Trigonal
Also called Rhombohedral, this system’s unit cell is a skewed cube, like a cube pushed from one corner. All sides are equal, and all angles are equal, but they are not 90°.
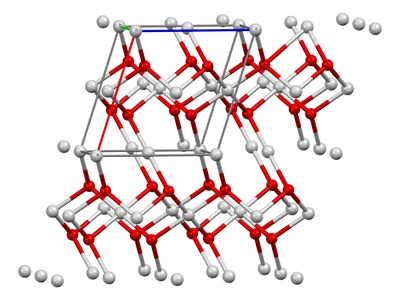
Monoclinic
This system is like a slanted rectangular box. It has three unequal axis lengths. Two of the angles are 90°, but the third is not, giving it an inclined shape.
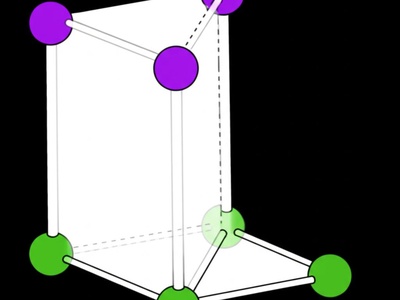
Triclinic
The least symmetric crystal system. None of the axis lengths are equal, and none of the angles are 90°. It has the most general shape possible for a unit cell.
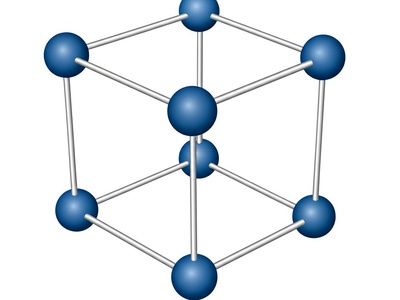
Simple Cubic (P)
The most basic crystal lattice with atoms only at the corners of a cubic unit cell. It is rare in nature due to its relatively poor packing efficiency (52% volume occupied).

Body-Centered Cubic (BCC)
This structure has atoms at all corners of a cube plus one atom in the very center. It’s common in strong, hard metals and balances strength with decent packing efficiency.

Face-Centered Cubic (FCC)
Features atoms at all corners and in the center of each of the six faces of the cube. Along with HCP, this is one of the two densest ways to pack spheres (74% efficiency).
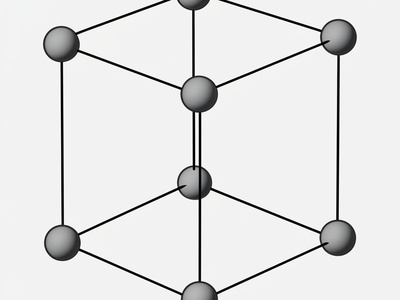
Simple Tetragonal
A lattice with points only at the corners of a tetragonal prism (a stretched cube). This is a geometrically possible but not commonly observed lattice for pure elements.
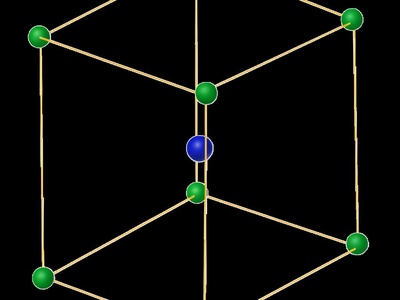
Body-Centered Tetragonal
A tetragonal prism with an additional lattice point at its absolute center. It’s like a BCC lattice that has been stretched or compressed along one of its axes.
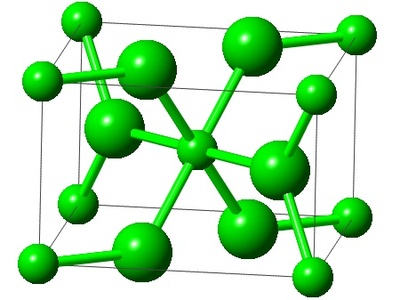
Simple Orthorhombic
The simplest orthorhombic lattice, with points only at the corners of a rectangular prism with unequal sides (a, b, c). It is found in a few elements and compounds.
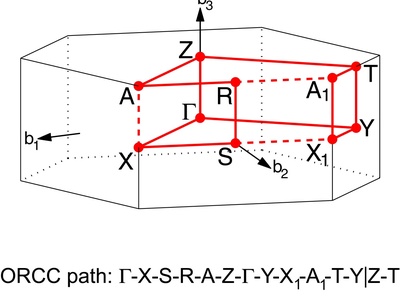
Base-Centered Orthorhombic
An orthorhombic lattice with points at the corners and in the center of two opposite faces. This allows for specific stacking arrangements not possible in other orthorhombic lattices.
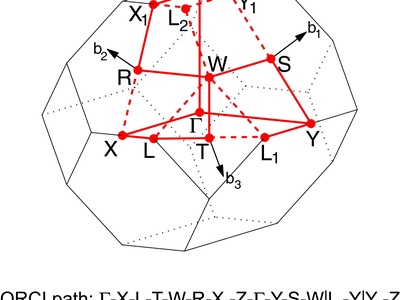
Body-Centered Orthorhombic
An orthorhombic lattice with points at the corners and one additional point in the geometric center of the rectangular prism unit cell.
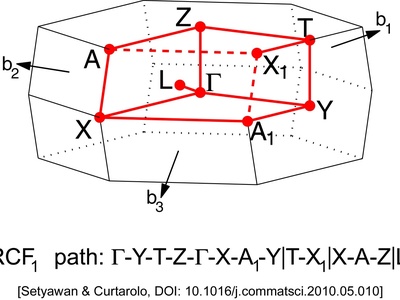
Face-Centered Orthorhombic
The most complex orthorhombic lattice, featuring points at all eight corners and in the center of all six faces of the rectangular prism cell.

Hexagonal
The fundamental lattice for the hexagonal system, consisting of a prism with a hexagonal base. It forms the basis for the very common Hexagonal Close-Packed (HCP) structure.
Rhombohedral
The primitive cell for the Trigonal system is a rhombohedron, which is a six-sided shape where all faces are identical rhombi. It can be visualized as a distorted cube.
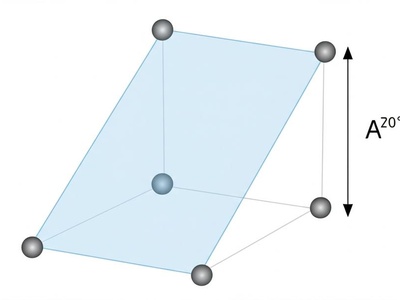
Simple Monoclinic
The basic monoclinic lattice with points only at the corners of the unit cell, which is a prism with a parallelogram base and one non-90° angle.
Base-Centered Monoclinic
A monoclinic lattice with points at the corners and in the center of the two bases (the parallelogram-shaped faces). This is a very common lattice type for monoclinic minerals.

Triclinic
The only Bravais lattice for the triclinic system. It has points only at the corners of the most general unit cell, with no restrictions on axis lengths or angles.

Hexagonal Close-Packed (HCP)
One of the two densest sphere-packing structures (with FCC), characterized by an ABAB stacking sequence of hexagonal layers. It is very common in metals.

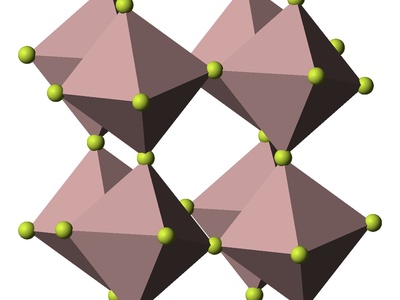
Diamond Cubic
Two interpenetrating FCC lattices, with all atoms being of the same element. Each atom is tetrahedrally bonded to four neighbors, resulting in a very strong but open structure.

Rocksalt (NaCl)
Composed of two interpenetrating FCC sublattices, one for cations and one for anions. Each ion is surrounded by six neighbors of the opposite charge in a perfect octahedron.
Cesium Chloride (CsCl)
A simple structure with one type of ion at the corners of a cube and an ion of the other type in the center. Each ion is surrounded by eight neighbors of the opposite charge.

Zincblende (ZnS)
A structure where cations occupy one FCC sublattice and anions occupy another, shifted relative to the first. Each atom is tetrahedrally bonded to four atoms of the other type.
Wurtzite (ZnS)
The hexagonal alternative to the cubic zincblende structure. It also features tetrahedral bonding, but the overall crystal has hexagonal symmetry. It’s common in many semiconductors.

Fluorite (CaF2)
A structure for AX2 compounds. The cations (Ca) form an FCC lattice, while the anions (F) occupy all the tetrahedral holes, resulting in 8-coordination for cations and 4 for anions.
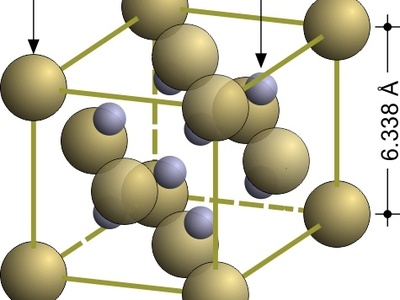
Antifluorite
The inverse of the fluorite structure, used for A2X compounds. The anions (O) form an FCC lattice, and the cations (K) occupy all the tetrahedral holes.
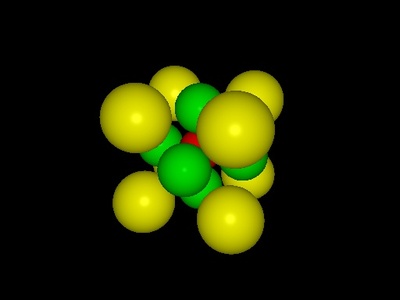
Perovskite (ABX3)
A cornerstone structure for functional materials. It has a large A-cation at cube corners, a smaller B-cation at the body center, and X anions (often oxygen) at the face centers.
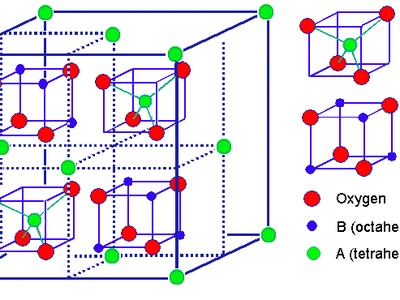
Spinel (AB2O4)
A complex but common oxide structure based on an FCC lattice of oxygen anions. The A and B cations occupy some of the available tetrahedral and octahedral interstitial sites.

Rutile (TiO2)
A common structure for AX2 compounds. It features cations in a distorted body-centered arrangement, with each cation octahedrally coordinated to six anions.