In the fascinating realm of mathematics, numbers often hold more depth than their simple appearance suggests. While many quantities are neatly expressed as whole numbers or fractions, there’s a unique category that stretches beyond these familiar boundaries, extending infinitely without repeating.
This curated list delves into Irrational Numbers, those captivating quantities that cannot be written as a simple fraction. Here, we present 20 distinct examples, showcasing their diverse nature from the famously complex `2^{√2}` to the more common cubic root `∛2`. For each entry, you’ll find below its Approximate Value, its mathematical Type, and its Significance, offering a clear snapshot of its place in the numerical landscape.
What exactly makes a number irrational?
An irrational number is any real number that cannot be expressed as a simple fraction, meaning it cannot be written as a ratio p/q where p and q are integers and q is not zero. When written in decimal form, irrational numbers have non-repeating, non-terminating digits, extending infinitely without any discernible pattern.
Where do irrational numbers appear in the real world or in advanced math?
Beyond abstract theory, irrational numbers are fundamental in various fields. Constants like pi (π) are essential in geometry and engineering, appearing in everything from circle calculations to wave physics. The golden ratio (φ) is observed in art, architecture, and natural patterns. Many square roots, such as √2, are crucial in construction and trigonometry, demonstrating that these numbers are not just mathematical curiosities but integral to understanding our physical environment.
Irrational Numbers
| Number/Symbol | Approximate Value | Type | Significance |
|---|---|---|---|
| √2 | 1.41 | Algebraic (quadratic irrational) | First known irrational; Pythagorean proof |
| √3 | 1.73 | Algebraic (quadratic irrational) | Appears in geometry; classical irrationality |
| √5 | 2.24 | Algebraic (quadratic irrational) | Related to golden ratio and Fibonacci numbers |
| ∛2 | 1.26 | Algebraic (degree 3 irrational) | Ancient “doubling the cube” problem |
| φ | 1.62 | Algebraic (quadratic irrational) | Ubiquitous in art, Fibonacci limit |
| Silver ratio (1+√2) | 2.41 | Algebraic (quadratic irrational) | Continued fraction and Pell connections |
| Plastic constant ρ | 1.32 | Algebraic (degree 3 irrational) | Root of x^3=x+1; Padovan sequence |
| Tribonacci constant | 1.84 | Algebraic (degree 3 irrational) | Limit ratio of Tribonacci sequence |
| √2+√3 | 3.15 | Algebraic (degree 4 irrational) | Sum of quadratics gives algebraic irrational |
| √7 | 2.65 | Algebraic (quadratic irrational) | Representative square-root of a prime |
| π | 3.14 | Transcendental | Circle constant; transcendence proved by Lindemann |
| e | 2.72 | Transcendental | Base of natural logarithms; calculus cornerstone |
| ln2 | 0.69 | Transcendental | Logarithm of 2; transcendence via Lindemann |
| e^π | 23.14 | Transcendental | Gelfond’s constant; Gelfond–Schneider theorem example |
| 2^{√2} | 2.67 | Transcendental | Classic Gelfond–Schneider example of transcendence |
| Liouville’s constant | 0.11 | Transcendental | First explicit transcendental number constructed by Liouville |
| Apery’s constant ζ(3) | 1.20 | Irrational (transcendence unknown) | Proved irrational by Apéry in 1979; zeta value |
| ζ(2)=π^2/6 | 1.64 | Transcendental | Euler’s Basel problem result connecting series and π |
| π^2 | 9.87 | Transcendental | Fundamental in series, integrals, and physics |
| √11 | 3.32 | Algebraic (quadratic irrational) | Another prime square-root example used in number theory |
Images and Descriptions

√2
The length of the diagonal of a unit square; historically the first number proved irrational by ancient Greeks. Its simple proof and continued-fraction expansion make it the central introductory example in number theory and geometry.

√3
Arises as the height of an equilateral triangle with unit side; √3 is irrational with elementary proofs related to parity. It shows up in trigonometry, crystallography, and lattice problems across mathematics and physics.

√5
Connected to pentagon geometry and the closed form for Fibonacci numbers, √5 is irrational. It plays a key role in algebra, continued fractions, and classical geometry, linking number sequences to geometry.

∛2
The real cube root of two is an algebraic irrational of degree three and a centerpiece of classical construction problems. Its irrationality underlies the impossibility of doubling a cube with straightedge and compass.

φ
The golden ratio φ=(1+√5)/2 is irrational and appears in art, architecture, and nature. It equals the limit of consecutive Fibonacci ratios and has distinctive continued-fraction, algebraic, and geometric properties.

Silver ratio (1+√2)
Also called the silver ratio, 1+√2 has continued fraction [2;2,2,…]. This quadratic irrational appears in Pell equations, tiling, paperfolding sequences, and design proportions as a counterpart to the golden ratio.
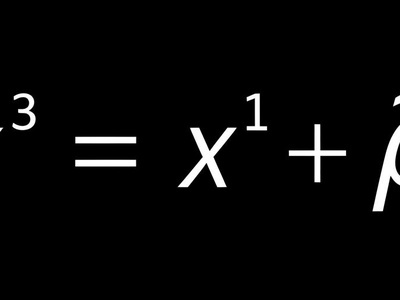
Plastic constant ρ
The plastic constant is the real root of x^3=x+1 and is an algebraic cubic irrational. It appears as the limiting ratio of Padovan and Perrin sequences and shows up in architectural proportion problems.
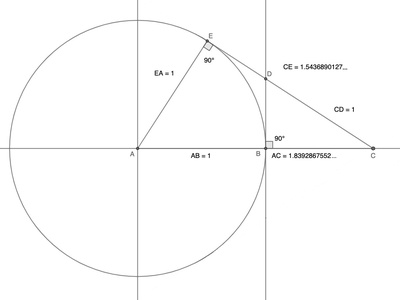
Tribonacci constant
The Tribonacci constant is the real root of x^3-x^2-x-1=0, giving the limiting ratio of the Tribonacci sequence. It is a natural cubic algebraic irrational that generalizes the Fibonacci limit idea.
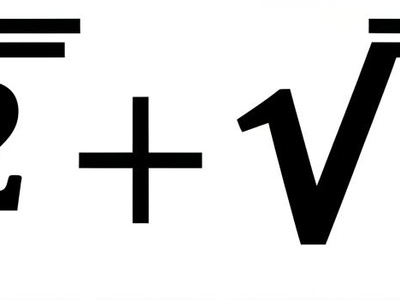
√2+√3
The sum √2+√3 is algebraic (degree four) and irrational. It illustrates how sums of simple irrational numbers can produce higher-degree algebraic numbers, arising in solving biquadratic equations and algebraic manipulations.

√7
Square root of seven is an elementary quadratic irrational and a standard example showing square roots of primes are irrational. It appears across Diophantine problems, geometry, and number theory examples.

π
π is the ratio of a circle’s circumference to its diameter, central to geometry and analysis. Proven irrational in the 18th century and transcendental by Lindemann in 1882, π’s properties shaped many mathematical developments.

e
Euler’s number e arises from compound growth and calculus; it was shown irrational by Euler and transcendental by Hermite. e underpins exponential growth, complex analysis, infinite series, and differential equations.

ln2
Natural logarithm of 2 is transcendental because algebraicity would contradict Lindemann’s theorem. ln2 appears in information theory, series expansions, harmonic sums, and many logarithmic identities across mathematics.

e^π
Known as Gelfond’s constant, e^π is a striking transcendental number produced by deep results in transcendence theory. It exemplifies how combining fundamental constants can yield numbers beyond algebraic description.

2^{√2}
The number 2^{√2} is a celebrated example from the Gelfond–Schneider theorem: an algebraic base raised to an algebraic irrational exponent can be transcendental. It highlighted modern transcendence theory.

Liouville’s constant
Constructed with ones at factorial places in its decimal expansion, Liouville’s constant was the first explicit number proved transcendental. It showed constructively that transcendental numbers exist in abundance and are well-approximable by rationals.
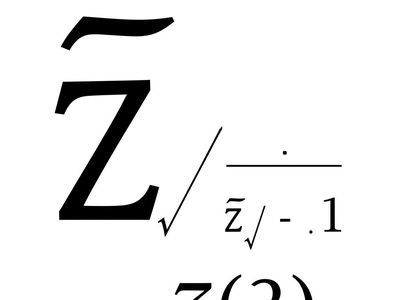
Apery’s constant ζ(3)
Apery’s constant equals the sum of reciprocals of cubes and was proved irrational in 1979, a surprising result in zeta-value arithmetic. Its transcendence remains an open problem in number theory.
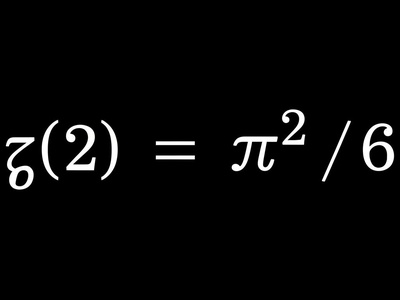
ζ(2)=π^2/6
ζ(2) equals π^2/6, solved by Euler in the 18th century. Because π is transcendental, ζ(2) is transcendental as well; this value links infinite series, geometry, and Fourier analysis.

π^2
Square of π appears in many classical formulas and series, such as ζ(2) and Fourier integrals. As a function of π, π^2 inherits transcendence and plays a central role in analysis and mathematical physics.

√11
Square root of eleven is a straightforward quadratic irrational illustrating that the square roots of non-square integers are irrational. It is commonly used in examples and problems in algebra and Diophantine equations.



